Budget Constraints (Micro Economics)

Micro Economics 

- Chapter 2. Budget Constraints

Economists assume that consumers choose the best bundle of goods they can *afford. To give content to this theory, we have to describe more precisely what we mean by “best” and what we mean by “can afford.”

* afford : 최적

we're going to start with our consumer theory. And the first topic we're going to see will be the budget and other constraints on choice. 

Set circumstances, given the goods that we would like to consume, let's say there are *a finite number of goods that we would like to enjoy consuming them, their prices and our income to spend on these goods, which goods or which collections of goods *will be affordable for us to buy and consume? 

* a finite number of goods : 한정된 재화
* will be affordable for us? : 적절화 될 수 있을까요?

Overview

1. Slope of the budget constraint (예산 제약의 기울기)

2. Comparative statistics analysis (비교 통계 분석)

: *Intuitively, that means that, let's say initially we had certain amount of income to spend on some particular goods, but now we have a different income. 
For example, We have a salary increase, or there may be changes in the prices of these goods, so how these changes affect the collections of the goods that we can afford. I also make another video in general about comparative statistics analysis because that's one of the very common analyses that we use. 
# Reality = exogenous variables & endogenous variables

*Intuitively : 직관적
*exogenous variables & endogenous variables : 외생 변수 & 내생 변수

3. Applications on tax or food stand(세금 또는 식품 가판대에 대한 몇 가지 응용)

Next, we'll talk a little bit about some applications on tax or food stand. We'll talk a little bit about *numeric goods, some *nonlinear budget standards. *constraints and conclude with general choices. 

*numeric goods : 수치 상품
*nonlinear budget standards : 비선형 예산 표준
*constraints : 제약 조건

So a consumption choice set is the collection of all consumption choices available to the consumer. But, there also exist constraints. So what *constraints consumption choice?
If, I can have some budget constraint, I don't have enough money probably to buy the whole supermarket. If I try to buy, lots of goods like the whole supermarket, definitely I won't have time to do that. 
There can be some other resource limitations that they will not allow me to do certain choices will not be available.

*consumption choice set : 소비 선택 집합
*constraints consumption choice : 소비 선택에 제약이 되는 것

Budget constraint

: Suppose that there is some set of goods from which the consumer can choose. In real life there are many goods to consume, but for our purposes it is convenient to consider only the case of two goods, since we can then depict the consumer’s choice behavior graphically.

{(x1, x2, ... , xn) | x1 ≧０.. xn ≧０& p1x1 + ... + pnxn = m} = budget constraint

Consumption bundle (x1, x2)

: This is simply a list of two numbers that tells us how much the consumer is choosing to consume of good 1, x1, and how much the consumer is choosing to consume of good 2, x2. Sometimes it is convenient to denote the consumer’s bundle by a single symbol like X, where X is simply an abbreviation for the list of two numbers (x1, x2). ※Caution, but has Constrain.
We suppose that we can observe the prices of the two goods, (p1,p2), = Commodity prices, and the amount of money the consumer has to spend, m, It refers the consumer's income to spend on these N different *commodities, and we do have these quantities that we mentioned and we are summing up all these N quantities by also multiplying those *quantities with their respective prices. (m : income maximum)

So, the budget constraint of the consumer can be written as p1x1 + p2x2 ≤ m. 
meaning, budget bundle < budget constraint.

2.3 Properties of the Budget Set

Buget line : p1x1 + p2x2 = m

Budget line slope : -p1/p2

point in the line = affordable

point on the line = just affordable

point out of the line = not affordable

We call this set of affordable consumption bundles at prices (p1,p2) and income m the Budget set of the consumer.

*commodities : 상품
* quantities : 량

according to the Budget line equation(=Budget constraints equation) : p1x1 + p2x2 = m, 

x2 = m/p2 - (p1/p2)x1

if, x1 ↑、x2 ↓、Exchange 有：we call this "Opportunity Cost"(기회비용).
Economists sometimes say that the slope of the budget line measures the opportunity cost of consuming good 1. In order to consume more of good 1 you have to give up some consumption of good 2. Giving up the opportunity to consume good 2 is the true economic cost of more good 1 consumption; and that cost is measured by the slope of the budget line.

How could we find out slope of Budget line?
Solve : if x1 increase 1, then x2 will -(p1/p2) the value,
            if x1 decrease 1, then x2 will (p1/p2) the value.

2.4 How the Budget Line Changes

Then, what if m changes? 

ex1. what means higher income?
        : Original Budget line will move →＆↑、with no slope(:-p1/p2) changes.

ex2. what means lower income?
        : Original Budget line will move ←＆↓、with no slope(:-p1/p2) changes.

If price of x1 changes, 

value of p1 increased, then budget line will move from m/p1 to m/pi. (←), slope = -pi/p2

value of p1 decreased, then budget line will move from m/pi to m/p1. (→), slope = -p1/p2

2.6 Taxes, Subsidies, and Rationing

Now well let's go over some applications from real life. If you buy Any item you typically pay this a sales tax. For instance in Korea, there is this uniform *Ed Valeram sales tax of 10 percent So whatever you buy actually 10 percent of the price On top of the price that you pay for the item is collected as this sales tax.
While here I do have a 5% example. 

*Ed Valeram sales tax : 간접세

if, 5% : (1+0.05)p = 1.05p

Original m/p2 & m/p1 will be m/(1+t)p2 & m/(1+t)p1.
according to this uniform Ed Valeram sales tax circumstances, Budget line equation(=Budget constraints equation) will move （←）＆（↓）

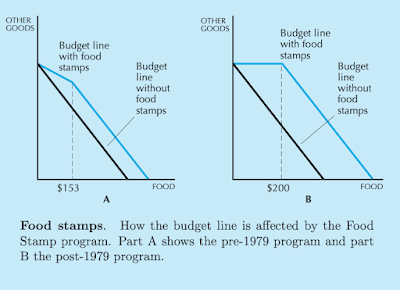
Another application that we're gonna have and play with this budget constraint and budget set ideas is the Food stamp programs. So food stamps are basically are some social programs there are families having tough economic situation And we don't want them to be left outside of the society, so we typically have, or the governments or the countries have policies to integrate those people to the society. basically these food stamps are coupons that can be legally exchanged only for food. 

Let's say we have two items, food which we denote by x1 and some other goods, x2, so whatever they are. And let's say that the family has hundred dollars and the price of these two items, food and the other goods, they're both one. So the question is let's say that this family now receives 40 units of food stamps of x2. 

In this situation, that as the consumer buys some food items up to the first 40 units, they don't need to give up any consumption of the other good because they don't use this $100(= m), but they are using simply the food stamps. So in particular point the slope is zero. (= means 'not linear shape' is possible)

Okay now so let's play with this story a little bit more and ask What if food stamps can be traded on a black market for 50 cents (=0.5 dollar) each? 

In this case, first draw the normal non-linear food stamps Budget constraint.
Second,  draw the line after in particular point of the slope is zero.

for example, if point m/p2 is 140, m/p1 is 100. then after Black market condition, m/p1 changes from 100 to 120

2.7 Budget Line Changes

: Numeraire changes change notthing. (but, useful for calculation)

ex.    p1=2    →    p1=200
         p2=3    →    p2=300
         m=12    →   m=1200

all, 2x1 + 3x2 = 12 , Budget line(=Budget constraints)

Shape of Budget constraints

Q. What makes a budget constraint a straight line?

Quantity discount :

if p2 = 1, but if ０≦ x2 ≦ 20, p2 = 2

shape of line will be not straight. & *concave shape

Quantity penalty :

if p2 = 1, but if ０≦ x2 ≦ 20, p2 = 0.5

shape of line will be not straight. & *convex shape

*concave shape : 오목한 형태
* convex shape : 볼록한 형태

Shape of Budget Constraints - One price Negative

ex. Commodity : garbage paid 2 dollar (쓰레기를 구매하면 2달러 +)

p1 = -2, p2 = 1, m=10

then, slope : -p1/p2 = 2, point : x2 = 10

Summary

1. The budget set consists of all bundles of goods that the consumer can afford at given prices and income. We will typically assume that there are only two goods, but this assumption is more general than it seems.

2. The budget line is written as p1x1 +p2x2 = m. It has a slope of −p1/p2, a vertical intercept of m/p2, and a horizontal intercept of m/p1.

3. Increasing income shifts the budget line outward. Increasing the price of good 1 makes the budget line steeper. Increasing the price of good 2 makes the budget line flatter.

4. Taxes, subsidies, and rationing change the slope and position of the budget line by changing the prices paid by the consumer.

[Reference]

[1] Hal R. Varian - Intermediate Microeconomics_ A Modern Approach, 8th Edition  -W.W. Norton & Co. (2010)